Modern Portfolio Theory (MPT) is a method to select which stocks and what amounts to buy such that as a group, these stocks give the highest amount of returns for a given amount of risk.
In this article, risk is defined as the volatility[2] of your returns[1].
[1] Returns are the money made or lost over a period of time.
[2] Volatility refers to returns that change rapidly and unexpectedly.
Understanding Modern Portfolio Theory
The 2 main ideas behind MPT are:
- Preference for higher reward per risk
- Risk cancellation
Preference for higher reward per risk
Let’s say you are betting at a casino and you have 2 games to choose from.
- In the first game, you gain $5 if you win. But if you lose, you’re out $3.
- In the second, you could win $5, but if you lose, you are down $1.
Assume that the odds of winning is the same for both games.
Which will you choose?
I hope you choose the second game. If you chose the first, please go ahead and close your trading account now.
This shows that for a given set of returns, we naturally want to risk as little as possible.
Similarly, if we were to compare 2 stocks with the same gain, we prefer the one with less volatility.
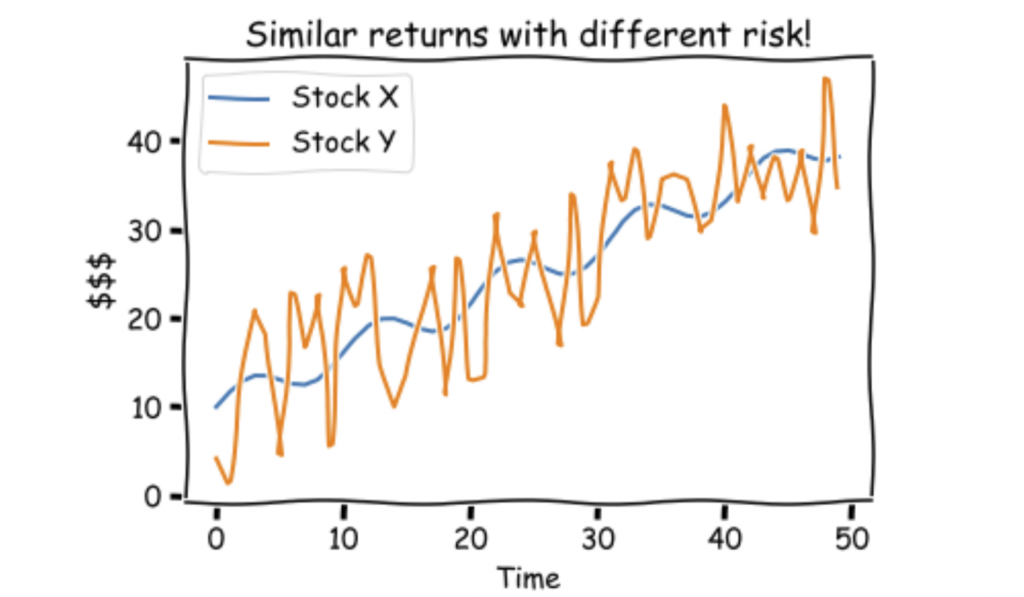
We prefer Stock X!
Risk cancellation
Let’s talk about stocks now.
To understand risk cancellation, we look at 2 stocks.
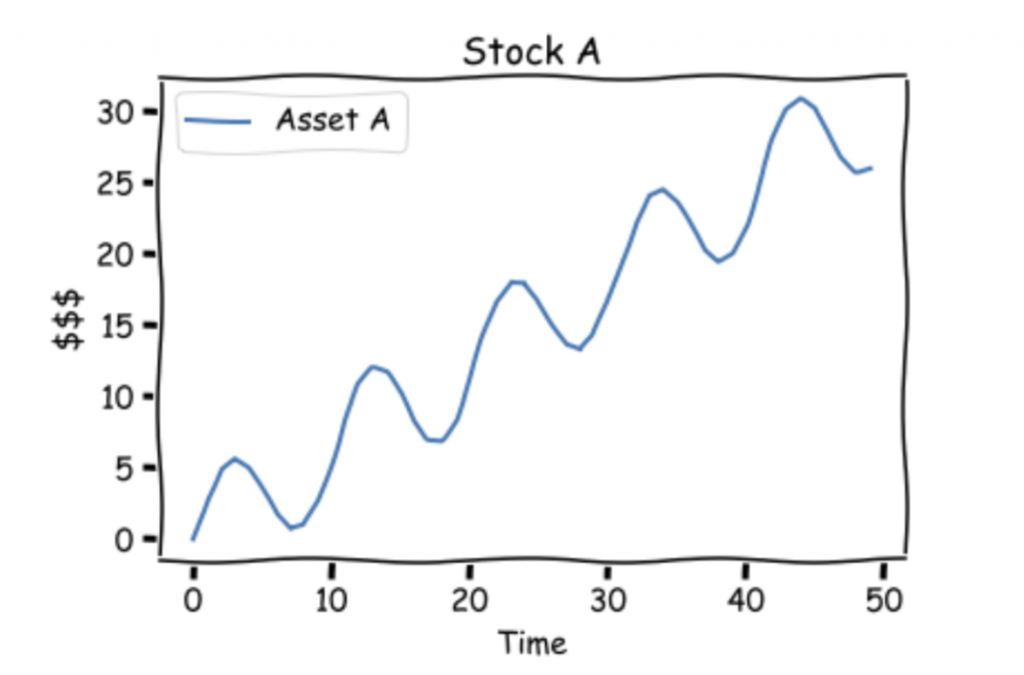
Stock A looks like this:
Stock B looks like this:
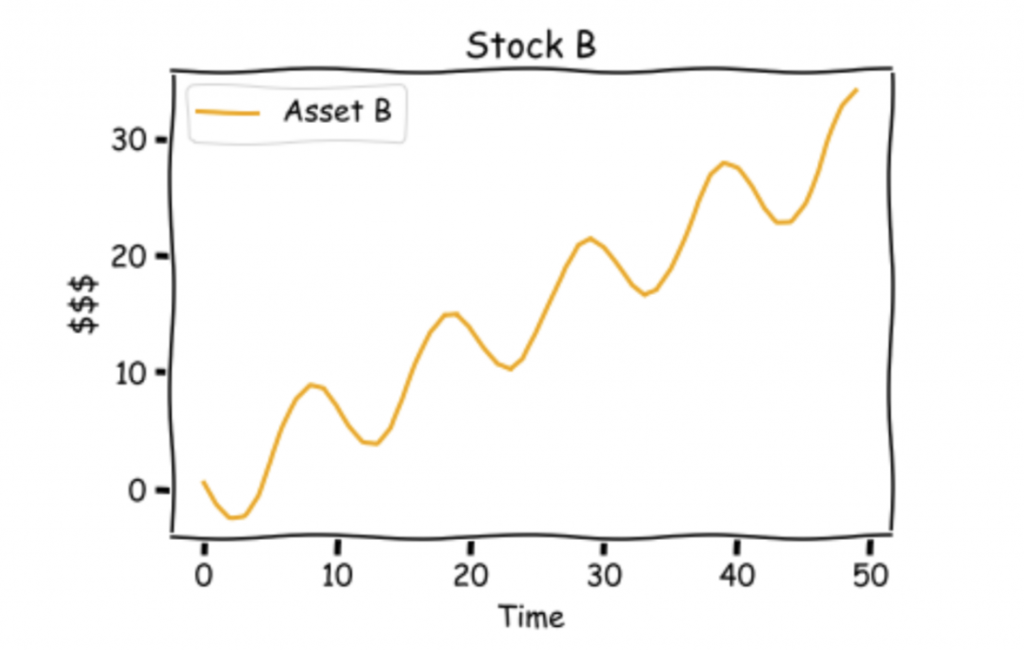
Both Stock A and B look similar. They both move up.
However, there is a difference, they are inversely correlated in the short run.
Combining Stock A and B
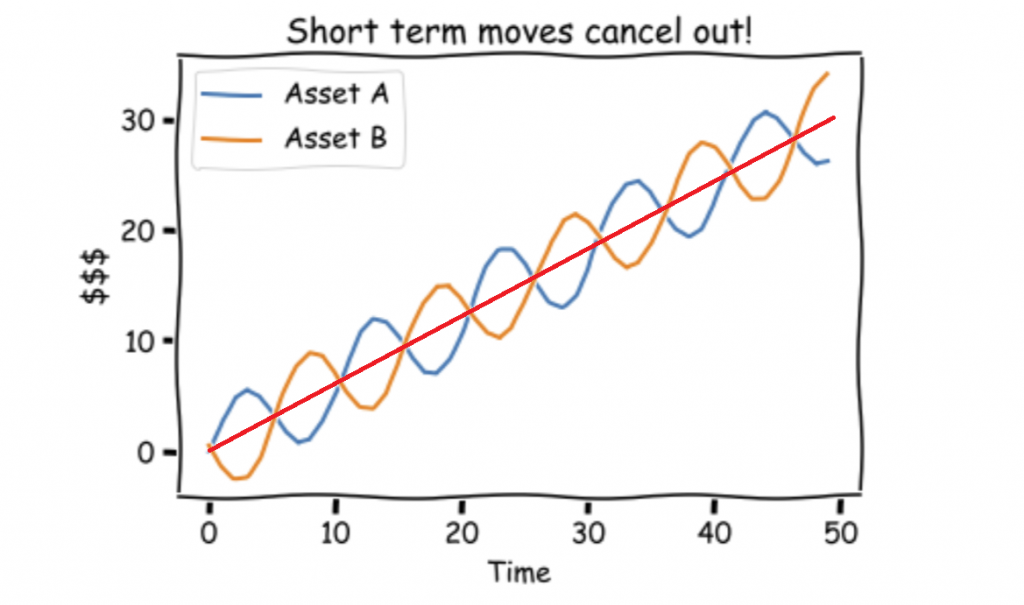
Both Stock A and B moves up at the same rate (i.e. have the same returns).
However, their short term moves cancel out.
As an example, if we own $50 of Stock A and $50 of Stock B, our $100 total investment can be represented by the red line.
The red line is better than owning $100 of either Stock A or Stock B alone as it is less volatile.
Remember we want the highest returns per risk (where risk is defined as the volatility of return).
So, what is MPT really?
MPT tells us to choose stocks in a way that their risks cancel out and that the overall returns are the highest for the amount of risk we take on.
Increasing stocks to cancel out more risks
One more concept of MPT is the required number of stocks for risk cancellation.
Using 2 stocks to cancel risks might not be ideal as it is difficult for the 2 stocks to be inversely correlated (in the short term) all the time.
If we have 3 stocks, it would be easier. If we have 4, it’s even easier.
However, each stock addition reduces risks to a lesser extent. The reason is, as our overall risk declines, there isn’t much risk left to eliminate.
Legendary hedge fund manager Ray Dalio describes this better than me: Ray Dalio breaks down his “Holy Grail”
A key takeaway from the video: Once you have about 10 assets in your portfolio, every additional asset provides minimal risk reduction.
One thing to note – when the risks to any individual stock are minimized, the main risk that is left is the exposure to the overall market movement.
Note that we use stocks in our examples but MPT applies to any asset – Commodities, Fixed Income, Forex, Cryptocurrency, etc.
Why is MPT important to you?
3 reasons.
Being able to size up to make more profits!
If your portfolio has low volatility, you will be able to increase your bet size without fear of losing it all.
Here is what happens when you double the amount you trade when your portfolio is volatile.
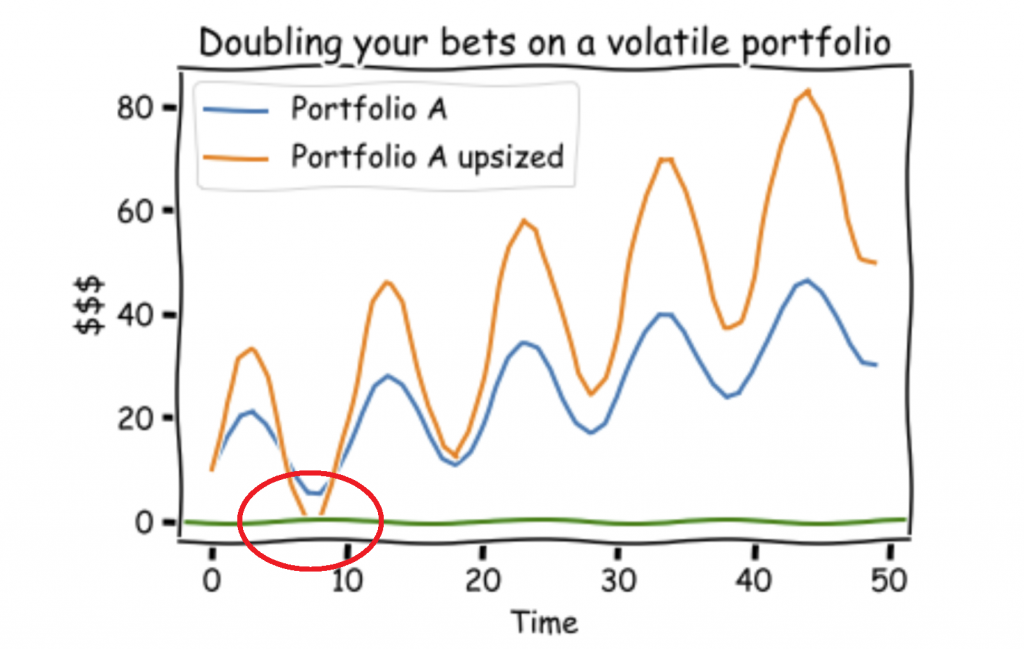
You hit $0 and get wiped out.
Here is what happens when you double the amount you trade when your portfolio is less volatile.
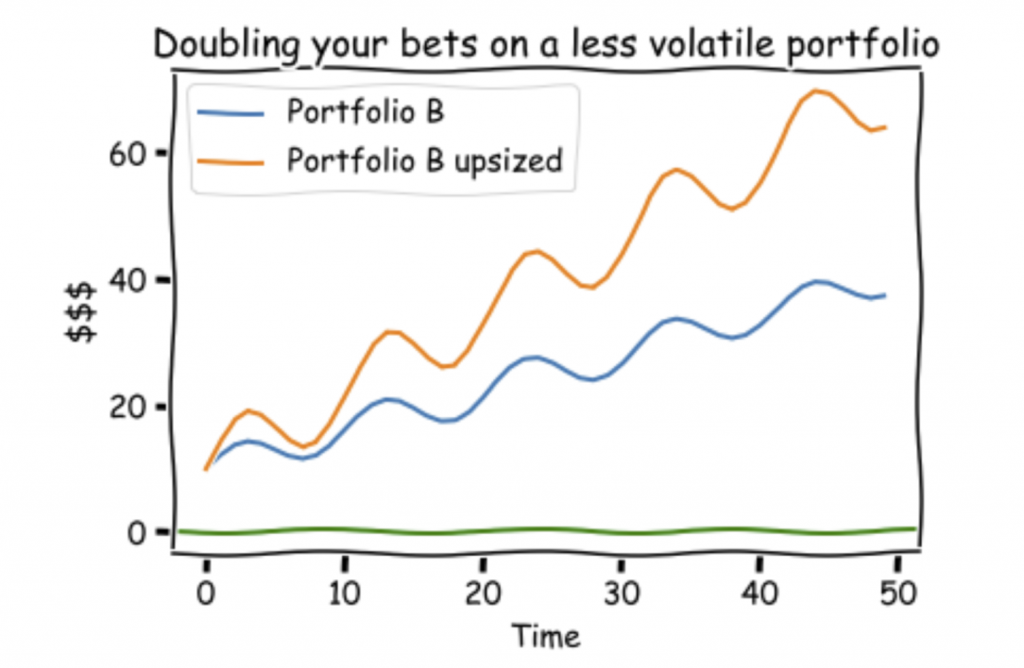
You stay in the game and make more monies!
Staying in the game
Even if your account does not hit zero. You might be in an unrecoverable position.
If you lose 50% need to make 100% to recover.
If your portfolio is worth $100 and you lose $90, you’ll only have $10 left. You need to make 1000% to hit $100 again.
Thus, if your returns are too volatile, you might not be able to recover.
Examples of Modern Portfolio Theory
Modern Portfolio theory has inspired certain specific portfolios such as the Ray Dalio All Weather Portfolio.